Decision Tree (의사결정 트리)

Decision Tree

AI를 이용한 마케팅 중, 백화점 앱에서 성별, 연령, 관심사, 구매 내역 등을 봤을 때 관련 상품을 할인하여 주는 쿠폰을 발송하는 이벤트를 종종 보곤 한다. 이 AI는 어떤 원리를 거쳐서 만들어진 것일까? (물론 다른 방법으로도 가능하지만, decision tree의 대표 예 중 하나를 든 것이다.)

Decision tree는 위에서부터 아래로(top-down) data에게 기준을 주어 질문을 한 뒤 원하는 class로 분류될 수 있도록, 또는 원하는 값을 찾을 수 있도록 하는 machine learning의 한 방식이다.

아주 basic한 Iris를 예로 들면, 꽃잎의 길이가 50cm가 넘는가? -> Yes 이면 setosa로 분류되는 것과 같은 방식이다. No라면, 꽃잎의 너비가 1.75cm 이상인가? 지표를 한번 더 통과시켜 versicolor인지, virginica인지 나누게 된다. 즉 트리의 마지막 (leaf node) 은 분류된 결과, class를 의미한다.

Decision tree는 해석이 쉽고 직관적이라는 장점이 있는 반면, 샘플 data로 decision tree를 구성하는 방식이기 때문에 샘플에 매우 민감하여 데이터가 사전에 설계한 것과 조금만 다르더라도 트리 구조가 바뀌게 된다.

용어를 정리해 보자면,

• Node : 분류의 기준이 되는 변수(독립변수라고 생각하면 된다.)가 위치하는 곳. node를 기준으로 샘플을 나누게 된다.
• Edge : 샘플을 분류한느 조건이 위치하는 곳
• Depth : Root node에서 특정 node까지 도달하기 위해 거쳐야 하는 edge의 수

독립변수가 continuous 하면 연속형 변수(회귀 트리)로, discrete하면 범주형 변수(분류 트리)로 구성할 수 있다.

나는 처음에 이 자료구조를 들었을 때, 이게 machine learning이 맞나? 솔직히 if-else로 나누는 것과 뭐가 다른가? 라고생각해 봤는데 사실 우리가 생각하는 deep learning 방식과는 다르게 black box가 들어간다는 느낌보다는, 수학적으로 계산하여 network를 설계한다는 점이 다르다고 볼 수 있다.

사실 이 알고리즘에서 가장 중요한 척도는 Node를 얼마나 효과적으로 나누느냐? 즉, tree가 너무 깊지 않으면서 얼마나 효과적인 지표로 범주에 도달할 수 있는가? 인데, 사람이 일일이 나누기에는 한계가 있고 machine learning의 목표로 기계가 이를 찾아낼 수 있도록 수학적인 접근으로 root node 및 하위 node 들을 구성하는 방법을 사용한다.

여기에는 두 가지 방법이 있다.

Information Gain을 이용하는 방법

여기서 entropy라는 개념이 필요하다. Entropy의 직관적 정의는 0또는 1일 확률이 최소, 0.5일 확률이 최대가 되게 하는 함수이다. Data Science 에서의 entropy는 "data가 얼마나 고루 섞여 있냐"를 나타내는 지표이다. 

Information Gain, 상위 node의 entropy에서 하위 node의 모든 entropy를 뺀 값 - 이 분류를 통해 얼마나 정보에 대한 이득을 얻었는지의 변별력을 나타내는 지표, 이 가장 큰 node를 root node로 삼는 것이다.

Gini Index를 이용하는 방법

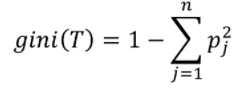
Gini Index는 통계학에서 사용되는 불평등의 정도를 나타내는 통계학적 지수로, 지니 계수가 높을수록 데이터가 분산되어 있음을 의미한다. 즉 Gini 계수가 낮을수록 구분이 확실하게 되는 것이다.

따라서, 각 class의 gini index를 계산하여 얻은 값 중 가장 낮은 것을 root node로 선정하게 된다.

 

Reference

https://medium.com/udacity/shannon-entropy-information-gain-and-picking-balls-from-buckets-5810d35d54b4

Shannon Entropy, Information Gain, and Picking Balls from Buckets